算出圆周率有什么用

*** 次数：1999998 已用完，请联系开发者***

揭秘:圆周率已精确至105万亿位,这项计算究竟有何意义?让我们对圆周率有全新的认识和理解。毫无疑问,人类对圆周率的追求将永不止步,因为隐藏在背后的是对宇宙本源和根本规律的孜孜以求。 不过,也有怀疑论者认为,圆周率再高精度的计算也不过是一个无限无尽的过程,并不意味着真正揭开了什么本质奥秘。毕竟数字和符号与宇宙的奥秘...

揭秘圆周率的无穷奥秘:科学家的解释让人豁然开朗圆周率的探索历程源远流长,可追溯至古代时期。古希腊数学家阿基米德是首位运用理论知识来近似计算圆周率的先驱者。 他以单位圆为切入点,从内接正六边形开始,踏上了艰辛的探索之旅。阿基米德先算出圆周率的下界,再凭借外接正六边形以及勾股定理求得上界。 此后,他持续增加多...

把圆周率继续算下去有何意义?科学家的解释,让人恍然大悟圆周率的探索历程源远流长,可追溯至古代。古希腊数学家阿基米德是首位运用理论知识来近似计算圆周率的先驱。 他从单位圆入手,以内接正六边形为起始点,开启了艰辛的探索之旅。阿基米德先算出圆周率的下界,再凭借外接正六边形及勾股定理求得上界。 此后,他持续增加多边形的边...

圆周率已计算至105万亿位,这究竟有何意义?让我们对圆周率有全新的认识和理解。毫无疑问,人类对圆周率的追求将永不止步,因为隐藏在背后的是对宇宙本源和根本规律的孜孜以求。 不过,也有怀疑论者认为,圆周率再高精度的计算也不过是一个无限无尽的过程,并不意味着真正揭开了什么本质奥秘。毕竟数字和符号与宇宙的奥秘...

圆周率已经算到105万亿位,计算圆周率到底有什么用呢?让我们对圆周率有全新的认识和理解。毫无疑问,人类对圆周率的追求将永不止步,因为隐藏在背后的是对宇宙本源和根本规律的孜孜以求。 不过,也有怀疑论者认为,圆周率再高精度的计算也不过是一个无限无尽的过程,并不意味着真正揭开了什么本质奥秘。毕竟数字和符号与宇宙的奥秘...

圆周率之谜:普朗克长度揭示的无限分割悖论这个问题颇具趣味性,首先来解答第一个问题:圆周率π是一个无穷无尽、永不重复的小数,它与进制无关。 在数学领域中,我们把π称为无理数,... π并没有什么神秘之处,每一个无理数背后都隐含着某种特定的几何关系。例如,一个单位边长的正方形,其对角线长度便是√2;又如,在60度的等...

●▽●

圆周率的尽头在哪里?普朗克长度揭示的极限与无限分割之谜这个问题颇具趣味性,首先来解答第一个问题:圆周率π是一个无穷无尽、永不重复的小数,它与进制无关。 在数学领域,我们把π称为无理数,这... π并没有什么神秘之处,每一个无理数背后都隐含着某种特定的几何关系。例如,一个单位边长的正方形,其对角线长度便是√2;又如,在60度的等...

╯▂╰

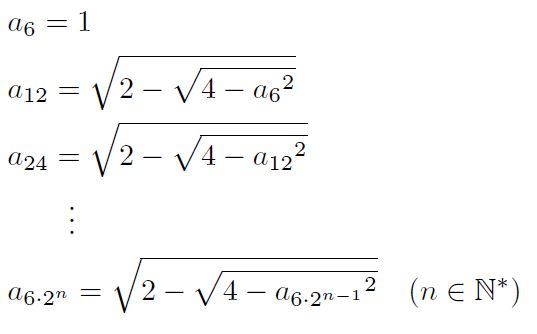
圆周率已算到105万亿位!人类为何如此执着地探索这个数字?在数学的浩瀚宇宙中,圆周率π无疑是一颗璀璨的明星。如今,圆周率已被算到 105 万亿位,这个惊人的数字背后,蕴含着人类无尽的执着与探索精神。那么,人类为何如此执着地探索这个看似普通却又无比神秘的数字呢? 首先,圆周率的计算具有重大的科学意义。在物理学中,圆周率与许多重...

≥▂≤ 圆周率的尽头:普朗克长度与无限分割之谜这个问题颇具趣味性,首先来解答第一个问题:圆周率π是一个无穷无尽、永不重复的小数,它与进制无关。 在数学领域中,我们把π称为无理数,... π并没有什么神秘之处;每一个无理数背后都隐藏着某种特定的几何关系。例如,在一个单位边长的正方形中,其对角线长度便是√2;而在60度的...

圆周率与普朗克长度的悖论:宇宙尺度之谜这个问题颇具趣味性,首先来解答第一个问题:圆周率π是一个无穷无尽、永不重复的小数,它与进制无关。 在数学领域中,我们把π称为无理数,... π并没有什么神秘之处,每一个无理数背后都隐含着某种特定的几何关系。例如,一个单位边长的正方形,其对角线长度便是√2;又如,在60度的等...